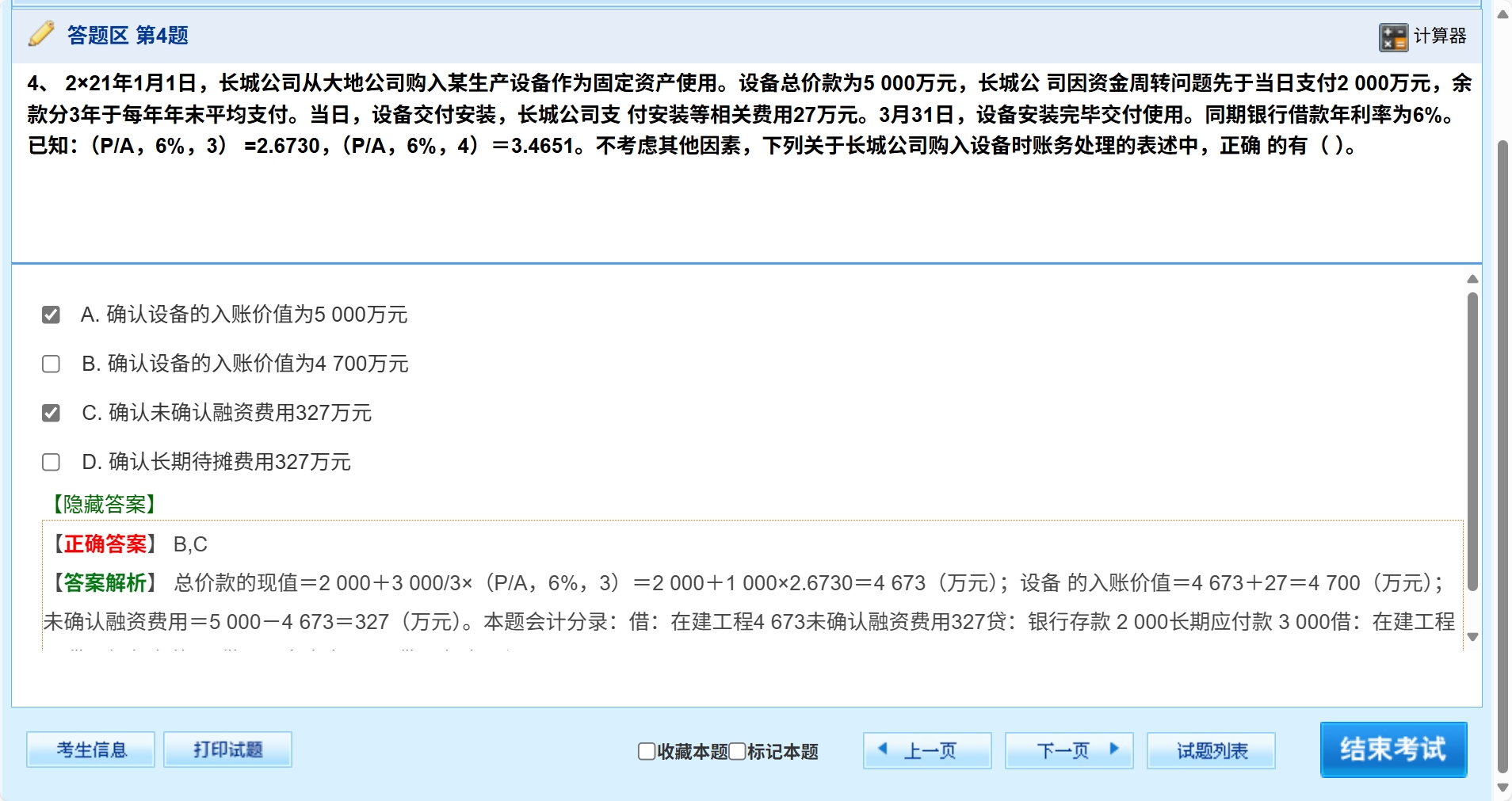
首先分析原理:
这里的 3000 万元是分 3 年于每年年末平均支付的款项。每年支付的金额 = 3000÷3 = 1000 万元 。
年金现值系数(P/A,i,n) 是用来计算等额系列收付款项在当前的现值。其中 i 是利率,n 是期数。
本题中每年支付的金额是 1000 万元,属于等额支付的年金形式,所以要计算这 3 年等额支付款项的现值,应该用每年支付的金额 1000 万元乘以年金现值系数(P/A,6%,3) ,也就是 3000÷3×(P/A,6%,3) ,而不是直接用 3000 万元乘以(P/A,6%,3) 。因为 3000 万元不是每年实际支付的金额,1000 万元才是每年等额支付的金额
首先分析原理:
这里的 3000 万元是分 3 年于每年年末平均支付的款项。每年支付的金额 = 3000÷3 = 1000 万元 。
年金现值系数(P/A,i,n) 是用来计算等额系列收付款项在当前的现值。其中 i 是利率,n 是期数。
本题中每年支付的金额是 1000 万元,属于等额支付的年金形式,所以要计算这 3 年等额支付款项的现值,应该用每年支付的金额 1000 万元乘以年金现值系数(P/A,6%,3) ,也就是 3000÷3×(P/A,6%,3) ,而不是直接用 3000 万元乘以(P/A,6%,3) 。因为 3000 万元不是每年实际支付的金额,1000 万元才是每年等额支付的金额
更多